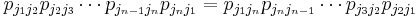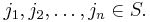Kolmogorov's criterion
In probability theory, Kolmogorov's criterion, named after Andrey Kolmogorov, is a theorem in Markov processes concerning stationary Markov chains (i.e. ones with stationary transition probabilities, also called "time-homogeneous Markov chains"). The theorem states that such a chain is reversible if and only if its transition probabilities satisfy
for all finite sequences of states
Here pij are elements of the transition matrix P and S is the state space of the chain.
Proofs of this theorem are available in the literature.[1]
Notes
- ^ F.P. Kelly (1979) Reversibility and Stochastic Networks, Wiley. ISBN 0471276014 p. 22